# math mtbos pixelart geometry maths proof stringtheory physics cube sphere circles nctm sketched secondgrade imissmykids scritturebrevi ventaglidiparole edtech mathedtech figurethat proofwithoutwords hsmath collegemath keynote everyonecancreate edchat appleedu appleeduchat isaacnewton classicalmechanics optics calculus circle mathed desmos funwithdesmos visualpattern patternlunch gsuiteedu mathchat ncsmsd2019 mathequity tangent

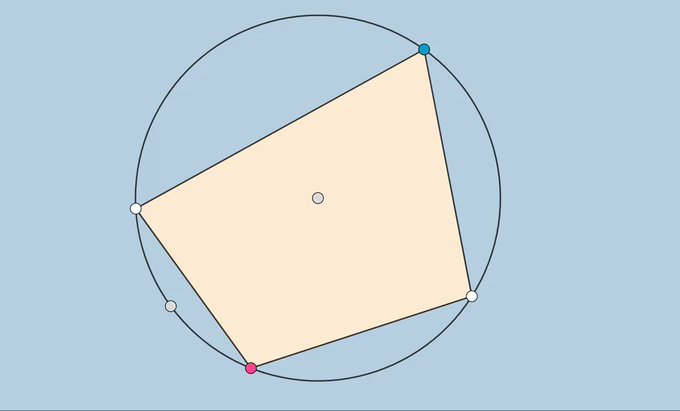
1 cyclic quadrilateral + 4 perpendiculars = 😮? How to prove? 🤔 Source: . https://t.co/XF5cVNRTkE

11 43
2020-12-21

1/
A local 2D cross-section of the real 6D manifold, known in as the Calabi-Yau quintic manifold.

In algebraic geom., a Calabi–Yau manifold is a particular type of manifold which has properties yielding applications in theoretical

Img: Wiki

29 74
2020-09-10

1 triangle + 1 cevian + 3 circumcenters = 4 concyclic points! How to prove? 🤔 Source: . https://t.co/rRs3VoE0Y1

4 15
2020-07-09

Stereographic projection of circles by .

Consider the 8 vertices of the as points on the unit then make (spherical) centered on those points with radii chosen so that the circles are just tangent.

More➡️https://t.co/NjifiSyj0Y


16 36
2020-06-16

This was so fun last year, we used 's idea for his skee ball problem that I got from his session. Thanks Zak. It was such a fun task- I it. I love how their solutions looked so different ⚾️🥎🏀⚽️#secondgrade

1 2
2020-05-02

"...it's a mysterious and marvelous fact that our universe obeys laws of nature that always turn out to be expressible in the language of calculus as sentences called differential equations."

- , 'Infinite Powers'.



54 139
2020-04-29

🌊Diving for Numbers🥽 This animation is a SUPER fun way to get you feet WET with addition! Grab the file to make your own changes!

Get the file here - https://t.co/NJwE8CVoOn

3 13
2020-03-13

was born on Jan 4, 1643 (acc. to Gregorian calendar).
A key figure in the scientific revolution, his 'Principia Mathematica' laid the foundations of

He made seminal contributions to and co-developed with Leibniz.

23 53
2020-01-05

Added a few more characters (PigPen, Woodstock, & Sally) to this year's holiday Peanuts dance. 🙂 https://t.co/bf8fDV4TV7

7 27
2019-12-26

Playing around with pattern tiles again this morning and found something *super* cool!

I started by making this from ... (1/many)

6 11
2019-09-02

The Chromebook Classroom Podcast: Teaching Math with Chromebooks https://t.co/0DpC4LvuAT

1 0
2019-05-01

Today we tried & ’s skeeball problem. They ❤️‘d it. I ❤️’d the variety of ways they organized their thinking 🤔 They know they can find more ways & R going 2 work on it at home 💕🌟

4 18
2019-04-11

How will you approach your mathematicians Monday? Thank you & ❤️💡🎾 I loved the story, Infinity & Me. I’m going to try this in 2nd. I changed the numbers, and I’m going to ask them to reflect too.

1 4
2019-04-05