Robert Fathauerさんのイラストまとめ

Here's a larger patch of the new aperiodic monotile with tiles rendered as shirts. The shirts without buttons are flipped over (mirrored tile shape). Each of the six possible rotational orientations is given its own color.

Mapping by Peichang Ouyang of a frog tessellation of mine

Decorating trapezoidal tiles to generate a spiral analog of the Cairo pentagon tiling

Spiraling rings design created by decorating tiles in a spiral tiling of trapezoids. Each tile has the same markings except for colors, which permute with a period of three tiles.

Correction, n = 3 also allows a second distinct matching.

n-armed spiral tilings of trapezoids based on regular n-gons. When n = 4 the trapezoid becomes a rectangle. Note that n = 5 is unique in allowing two distinct ways of matching adjacent scaled tiles.

Walkable trefoil knot, with handrails. Manipulate it here: https://t.co/gUIMHCMRF6

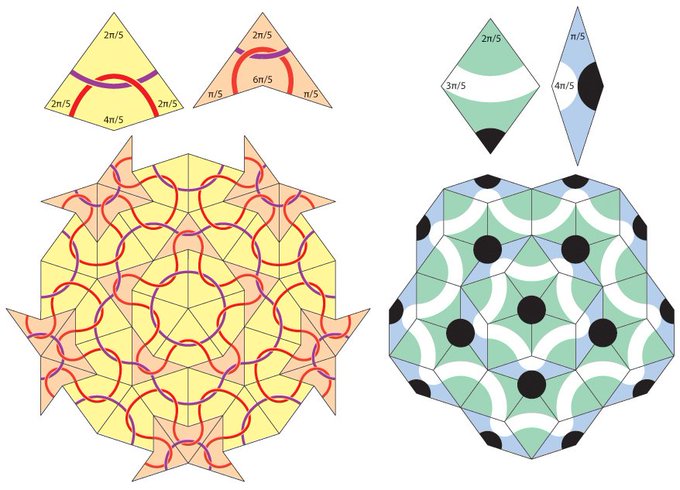
Writing a chapter on aperiodic tiling I've fallen in love with Penrose tiles all over again. Here are patches of both the kite-and-dart and rhombi versions of the tiles. The markings enforce matching rules.

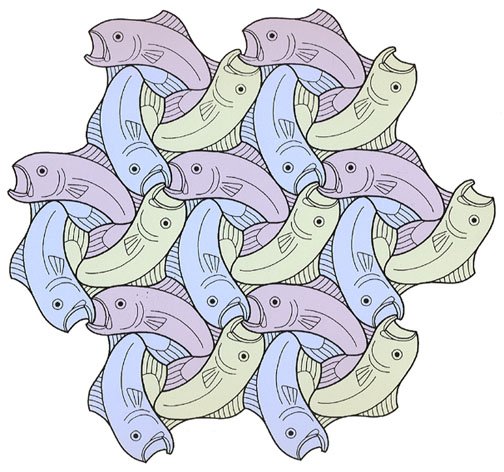
An exhibition of M.C. Escher's work opens tomorrow in Porto, Portugal: https://t.co/DQcR10261g. In addition to over 100 works by Escher, my "Three Fishes" screen print, from 1994, and some other contemporary tessellations will be on display. The exhibition runs through late July.

A variety of 2D tessellations are revealed by slicing a 3D tessellation of cubes, including the regular triangle tessellation and a semi-regular tessellation of hexagons and triangles.