Tiling Botさんのイラストまとめ

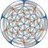
#Spherical #tiling shown rotating in the Mercator projection. Catalan tiling dual to omnitruncated {3,3}.

The edge coloring suggests another way to look at this tiling... as a triple compound of two tetrahedra and a cube. Thank you @sarahsmileatx for input on this one!

#Hyperbolic #tiling shown in the Joukowsky projection. Truncated {12,3}.

#Hyperbolic #tiling undergoing a limit rotation in the hemisphere model. Regular {3,∞}.

#Spherical #tiling shown rotating in the gnomonic model. Catalan tiling dual to truncated dodecahedron.

Growing/shrinking a hyperbolic heptagon to yield a continuous transition between {7,3} and {7,27} #hyperbolic #tilings.

#Twisty #puzzle guest tweet. #Hyperbolic #Rubik's cube analogue shown solving in the Poincaré disk model. 24-color puzzle based on the regular {7,3} #tiling. https://t.co/fH15fczvKw

#Hyperbolic #tiling with [8,3] #symmetry, shown uncentered in the band model. All mirrors of the fundamental triangle are active (omnitruncated).

#Hyperbolic #tiling with [19,5] #symmetry, shown uncentered in the orthographic model. Second and third mirrors of the fundamental triangle are active (bitruncation).