Tim Brzezinskiさんのイラストまとめ

What #geometry theorem(s) are dynamically illustrated here? Points moveable: https://t.co/l58IweqxMs. @geogebra #MTBoS #ITeachMath #math #maths #proof #EdTech #MathEd #HSMath

sin(2v) = 2*sin(v)*cos(v): Dynamic & modifiable illustration using equal areas. For a quick investigation for Ss (w/o ID appearing at the end): https://t.co/hIaGZcseR3. @geogebra #MTBoS #ITeachMath #math #maths #EdTech #trig #trigonometry #precalc #MathChat #HSMath #CollegeMath

Here, a @geogebra animation of @panlepan's problem posed earlier this week: https://t.co/bTIh6QYMcT.
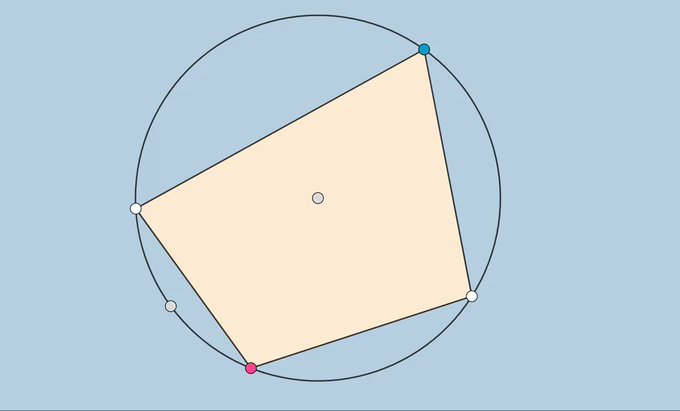
How can we formally prove the sum of these 2 square areas = 4*R^2, no matter where the large points lie? 🤔 #MTBoS #ITeachMath #geometry #math #maths #FigureThat #EdTech

@Cshearer41 @doubleroot @HRK2 @ilarrosac @panlepan Hey Catriona, I'll upload this @geogebra animation either later this week or early next (where users can change size of white regular hexagon and move intersection of yellow and orange regular hexagons). Great problem!

Inspired by @Cshearer41: For any RT, build a rectangle off its HYP so ratio of its L to W = 1:2. What is the measure of the pink angle? More importantly, WHY does this value NEVER CHANGE? https://t.co/wl2ZOWg42N @geogebra #MTBoS #ITeachMath #EdTech #math #maths #geometry #proof

SSS (Side-Side-Side) #Triangle Congruence #Theorem: Dynamic #Proof via Transformational #Geometry, SAS & 1 other theorem. Question: Which one? 🤔 https://t.co/bdKZuzNJXK. @geogebra #MTBoS #ITeachMath #math #maths #geometry #EdTech #MSMath #HSMath

#TriangleSurprise! When we build equilateral triangles off 2 sides of ANY TRIANGLE, another equilateral triangle surprisingly emerges! 😮 Why does this occur? 🤔Source: @gogeometry. Created with @geogebra: https://t.co/lTfrId4Hik. #geometry #math #MTBoS #ITeachMath #maths #EdTech

Similarity in Right Triangles: Dynamic Illustrations w/o Words. Created with @geogebra: https://t.co/Tm8i9UPsgP. Shout out to @KarenCampe for her suggestions to help me improve this 1st version: https://t.co/QZzxluxqsJ. #MTBoS #ITeachMath #EdTech#math #maths #geometry #proof

#FunFact: The common external tangent segment connecting any 2 tangent circles has a length equal to the GEOMETRIC MEAN of the radii of both circles. 😯 How to prove? 🤔(Source: @gogeometry). https://t.co/3RwqD4ki5M @geogebra #MTBoS #ITeachMath #geometry #proof #EdTech #math

#FunFact: Suppose V = a triangle vertex, I = incenter, O = orthocenter, & C = circumcenter. Then ray VI ALWAYS BISECTS angle OVC! How can we formally prove this phenomenon true? (Source: @gogeometry). https://t.co/rYmoDjwCNy @geogebra #MTBoS #ITeachMath #geometry #math #maths