Dave Richesonさんのイラストまとめ

The famous four color theorem says that you can color any map on the sphere with four or fewer colors. There's a similar result for every surface. For a torus, a map may require as many as seven colors, such as this one. Each of the seven "countries" borders every other country.

I did something different for the last pursuit curve. For this one I was imagining a dog on a leash perpendicular to the sidewalk (the red line) along which its human is walking. The human starts walking and the dog walks toward them with the leash taut (the leash is in light 5/6

I decided to redo the figure but starting with an equilateral triangle instead of a square—also lovely. Then, I took six of these triangles, reflected three of them, and joined them together to make a hexagon. 4/6

I've seen this braid called a rickrack braid, named for the zig-zag rickrack trim used by tailors. I made mine with strips of paper.

pencil. Here are four examples of pencil clip art. One looks correct, one is pretty good, and the other two are totally wrong.

I was just playing around with some "string art." I have recently started rewatching Game of Thrones, and so I felt the urge to make some 7-pointed stars.

As I mentioned in my previous tweet, artists often aim to have their art sit inside the 60° cone of vision. It looks like Rafael did this. By the artists' rule of thumb, this means we should not see much distortion in the painting. So, if I did my work correctly, I thought 5/8

He observed that Rafael panted some globes off to the side as perfect spheres. But, for the same reason I gave in my thread, they should be non-circular ellipses. I decided to try using what I've learned about perspective drawing to figure out what elliptical shape 2/8

I was recently reminded of Gardner's Four Bug Problem. (That's Martin Gardner, not a green thumb looking to keep pests off plants.) The problem: Four bugs sit at the corners of a 10"x10" square. Each walks directly toward its (clockwise) neighbor with the same constant 1/2

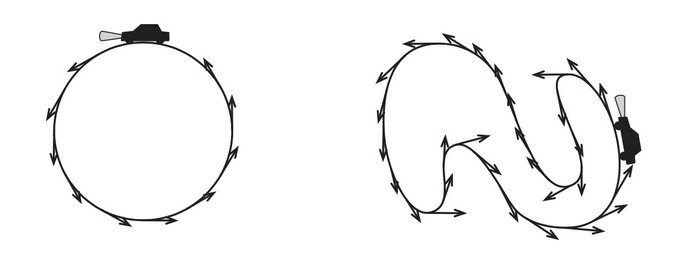
I watched some episodes of "Formula 1: Drive to Survive" on Netflix. Watching these races reminded me of the Theorem of Turning Tangents: the tangent vectors on a simple closed curve turn 360°. Intuitively, imagine a car driving counterclockwise around a Grant Prix track (you 1/4