Gabriel Peyréさんのイラストまとめ

Comparing 2D linear interpolation methods of order 0, 1 and 3. https://t.co/BDMDLQuoXF

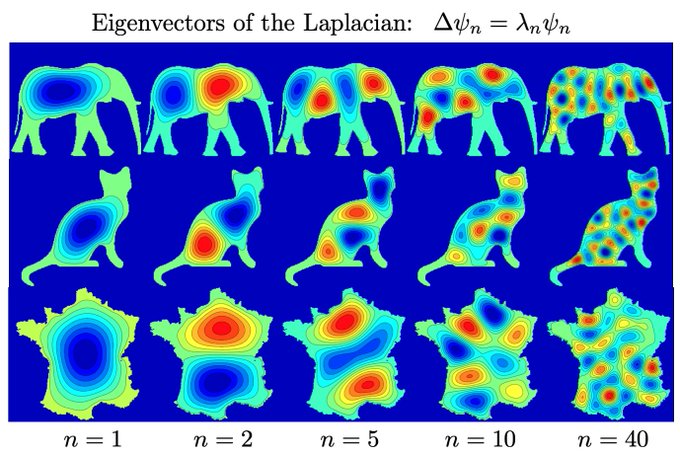
Eigenvectors of the Laplacian on compact planar domains define an orthogonal basis of oscillating functions, which generalize Fourier sinusoids. https://t.co/uEUf57QT8n

Edge collapse is a fundamental mesh processing primitive, at the heart of many mesh simplification methods. Influential papers by Hoppe, Garland and Heckbert.
https://t.co/Fp5rQyDtRf https://t.co/LPjMdAjPyy

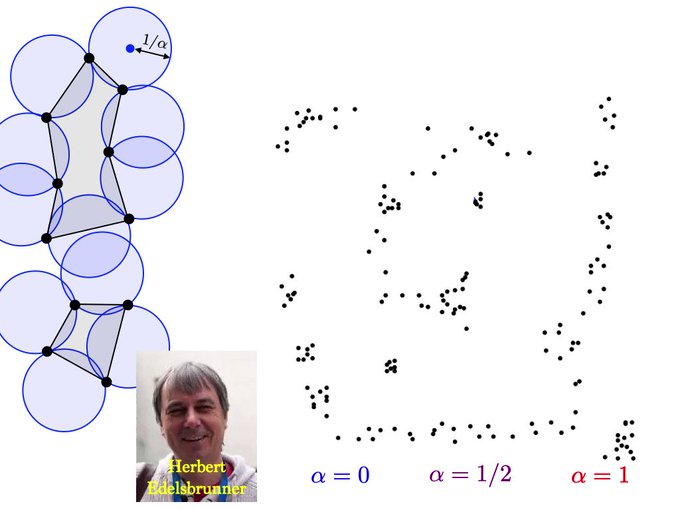
Alpha-shapes is a multiscale family of simplicial complexes included in the Delaunay which generalizes convex hull and is useful for topological data analysis and shape reconstruction. https://t.co/jGOB7yh4oN