体積のTwitterイラスト検索結果。 335 件中 7ページ目

確かに自分の体積が増えていてしょんぼりするまりちゃん

中学1年
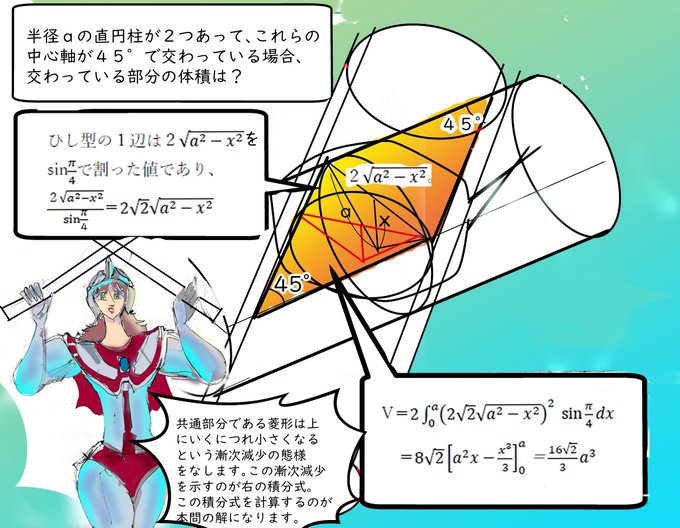
円錐と円柱、四角錐と四角柱などの
体積の求め方

体積の公式はここから！

#勉強垢さんと繋がりたい
#イラストレーターさんと繋がりたい
#イラスト好きと繋がりたい

@AYui777 @sonypotter #keisanサービス で #計算 した結果、#球体 の場合で直径62.035cmなら体積約125,000cm³となるわ(＾∀＾)プケラw
#密度 を #雪 と #氷 の中間である0.7(水が1.0)とすると、この雪合戦での決戦兵器と成りえる大玉の #質量(#重さ)は87.5kgねw
すると、気温0℃の時の #終端速度 は時速337.37kmに成るわw

#フォロー返します　#相互フォロー募集
#みんなで楽しむTwitter展覧会
#作品展示会　#アートミーム #創作エネルギー
#アートワーク #創作にゃんこ
#創作同盟 #アトリエの系譜
#digitalart　#ArtistOnTwitter　#ocart　#oc
#勉強垢　#大学受験　#体積　#volume　#断面形状
#数３ #積分　#integral

補助ボーン、アーマチュアの体積維持無し

前回の素体より格段に良くなった

綺麗なお尻の形を保ちながらウェイトを塗るコツをつかんだ💡

#3DCG #Blender #b3d

【水道管の破裂】
寒い夜に水道管が破裂することがあるよ。水は凍ると体積が増すからね。その防止方法のひとつが水抜き。
①水道の元栓を閉める
②全部の蛇口をひねり水を出し切る
③翌朝全部の蛇口を閉める
④元栓を開く
もし③を忘れちゃうと惨事だよ!!
※建物で多少異なる
https://t.co/wvcertWEQy

帽子とかで抑え込まれた体積以上のけも耳が 外したときに もふんっ！って 出てくる 「萌え」！

ダグラムにも車両が欲しいなあ。。。て思ってコミックのページめくってたらカッチョ良いのがデデーン！！！😄

戦闘指揮車

ザクッと高さ計算して1/72で作るとなると7cm超えになる事が判明。。。

デカい！

そっかあ。。。1/72って全てがデカいなあ。。。1/144の全てが倍の寸法、体積なら4倍。。。

この時期は体積が増えるこねっこ

ラスオリ、モンハン古龍種めいたメカドラゴンにスキン被せてエッッッお姉さんに仕立て上げるの体積とかそんなの関係ねぇ！氷系長命メカで案外気さくなお姉さん出すんだよ(見開き会議室テーブルﾄﾞﾝｯ)！！を幻視して一周回って感心しちゃった

フォトグラメトリ後のZbrush手順WIP
1 Blenderで上下位置出し
2 zbrushで不要面除去＆ミラーでZリメッシュ
3クレイポリッシュでノイズを更に除去
4 体積痩せた分を変形のコントラストで復元

ここから更にブラッシュアップとローポリ作り進行

バナッハ＝タルスキーのパラドックス【Banach-Tarski paradox】〔数〕球を3次元空間内で、有限個に分割し、回転・平行移動操作のみを使ってうまく組み替えることで、元の球と同じ半径の球を2つ作ることができるという定理。ただし各断片は通常の意味での体積を定義できない。

#ヴィラニスタート
体積変われば幼体化もできるかもって見たから…
好き勝手描かせてもろてます…ﾍﾍｯ

お題箱:ちいこいのち

ちいこいともえは冬になると体積が倍くらいになる

これはどう見てもイヤホンより2人の体積の方が大きい図 オグリもぺたん娘出て欲しい😪

しめ

最後にパッと思いつく欲しいものまとめて貼り
大体積むだろうからしばらくは買わないかな？、多分、きっと

「半分」なのが、体積なのか質量なのかは判らないが
大きさ以外の何かが「半分」であり、残り半分は「支えるべき肉体を持たない魄」なのではないだろうか
だから、「大きさを持たない」らしい魂とは異なり大きさは変わらずただ形だけが可変という

飢餓で縮むこともあると聞いて
失った体積回復中の図…

@Skydash827 キャラデをみたら、僕なら、多分こいう感じになるかな。違いは鼻の体積感の表現方法、邱さんはもうっとリアリティがある鼻に近い感じにしました。僕はもうっとキャラデでに近いアニメぽっく感じに、鼻穴を省略したやり方ですｗ

【額を丸くするのがなぜ理想とされるか】

額の体積が増えると顔下2/3との関係によって、
顔の重心が上に移動し、

『より小顔に、より女性らしく』

見えるようになる錯覚効果があります

横、斜めから見るとよく違いがわかります