マンデルブロのTwitterイラスト検索結果。 113 件
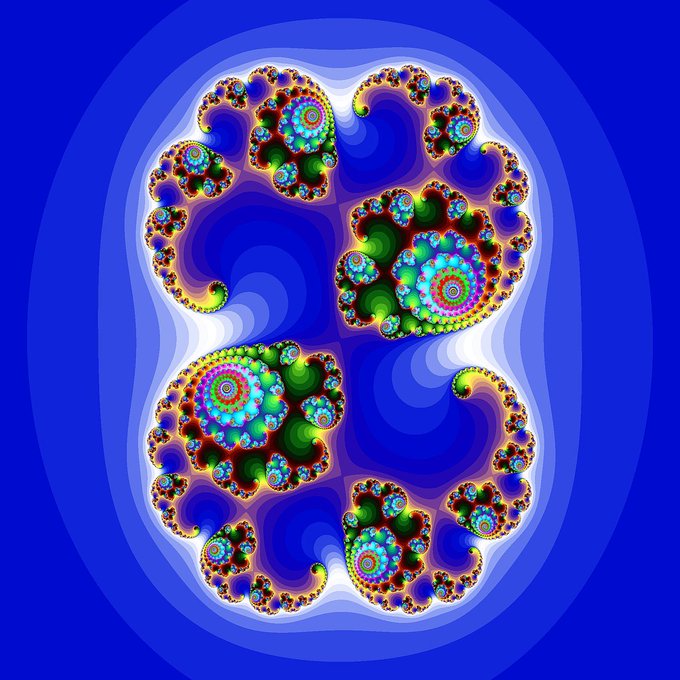
マンデルブロによる幾何学図フラクタルが気になっている
部分と全体が自己相似になってる図形
映画も1カット観ただけで全体の雰囲気や出来の良し悪しまで大体見当が付く
1カットじゃ物語の良し悪しまで分からないだろうが絵作りで作り手が世界をとらえる視点のクオリティは分かる
部分が全体を表す
0
8
部の展覧会にて大きなモニター上で自作のマンデルブロ集合アプリを実行するなどした.
2,3枚目は漸化式を少しいじったやつ.なかなか面白い発見が得られたし,細かい描画方法とかも語ることができて楽しかった.
2
15
こちらのマンデルブロ集合ビューア(Windows用ソフト)を使えば、マンデルブロ集合の好きな部分をひたすら拡大して描画/保存できて楽しいです!😺
この画像は初期配色ですが、配色が自由に変更できるので上手く調整すれば綺麗で映える1枚も撮れるかも😸
(色カスタムは一般のWeb版ビューアには無い機能…!) https://t.co/qPSG1O8pRu
3
17
一方、既知の2周期発散関数のマンデルブロ集合では、1点に集まる穴の個数は2個までのように見えます。(「1点に集まる穴の個数」は曖昧さを含んだ概念なので、はっきりしないケースもあります)
・c/(z^2-1)+1
・c(1/z-1/z^2)
1
6
.@oketsuiku5555 『マンデルブロ集合とジュリア集合 百合』
(Mandelbrot Set and Julia Set Lilies)
3
3