ほりたみゅ(bskyかmastodonに居ます)さんのイラストまとめ
@HyrodiumFollow @Hyrodiumさんをフォローする
Blueskyに移住しました。
bsky.app/profile/hyrodi…
hyrodium.github.io/jabsky.app/profile/hyrodi…
フォロー数：1697 フォロワー数：1962
26 件中 11〜20件を表示
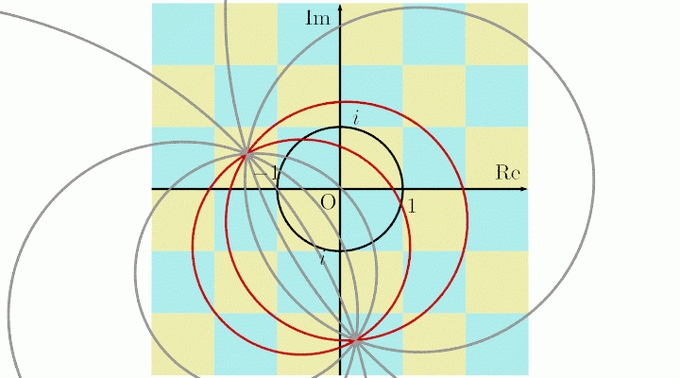
2円が交わる場合は, 円の族を原点を通る直線の族に移す一次分数変換がある. 直線の族はIm(log(z))の等高線になっている.
10
15
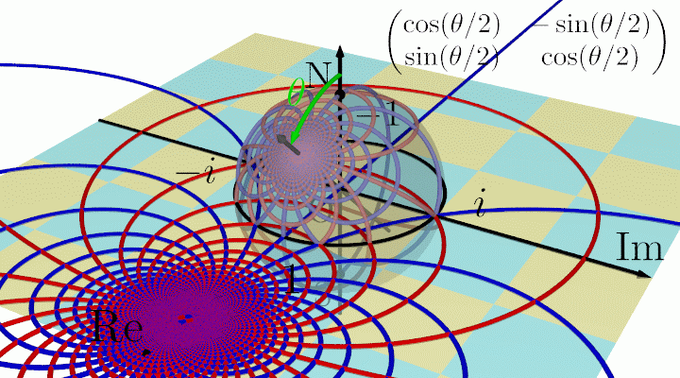
Im軸周りのθ回転を表すメビウス変換の行列Q(θ)はこのようになります. 良く知ってる2次元の回転行列と同じになります.
21
49
円を円に移す変換といえばメビウス変換です. 実はRe軸周りの任意の角θで回す変換を表す行列P(θ)は右上の行列になります. (計算ガリガリすれば確かめれる)
21
46
立体射影によって平面の広義の円は球面上の円に移される性質があったことから, (平面上の円)→(球面上の円)→(球面上の円)→(平面上の円)のように移されて1/zも円を描きます.
34
65
つまり, 複素数cの逆数はこのようにして[立体射影]→[Re軸で180°回転]→[立体射影]の手順で描く事が出来ます.
39
70