Jim Cobbさんのイラストまとめ

Playing with ellipses from a pencil of conics.

Combine contour and region plots: more intelligible. Note that asymptotes for the hyperbolas have same 60º/120º angles; some hyperbolas are singular; the fill created by Mathematica's RegionPlot has trouble dealing with singularities. Increasing MaxRecursion lessens the defects.

Explore another pencil of conics.

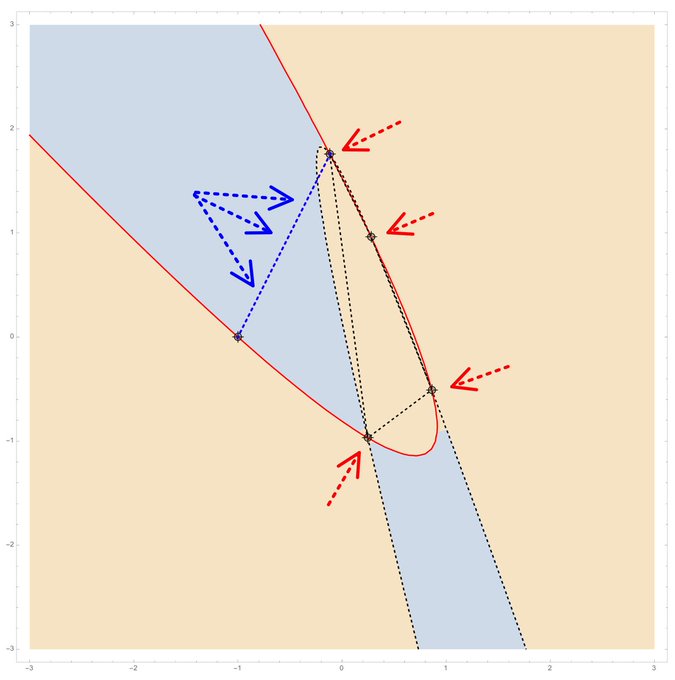
Each conic interpolates the four red points and is generated by one additional point to be interpolated. The boundary separating ellipses from hyperbolas is a pair of parabolas.

Five planar points in general position have a unique conic containing them. If the five points are vertices of a regular pentagon, the conic is a circle. Consider keeping four points fixed and letting one wander free. This is a one-dimensional linear system – a pencil of conics.

Logarithmic spiral arrangement of congruent annuli

Picnic table and attached bench in Evergreen Park – focus near, focus far

Packing cones…
Playing with conical yarn spools led me to use Mathematica to get a feel for the empty space uncovered by packed tangential truncated cones having parallel axes. I've spent decades pondering 3-D geometry, yet intuition still falls short.

@SamHartburn OK, I quit being lazy and got the exact values for the radii to be used in the construction. #DigitalGeometrySketchbook

@SamHartburn I like this. My version with Mathematica is a bit of a cheat: two radius values are trial and error values rather than exact solution from intersection calculations. I may go back and clean it up. I drew this using four disks and three annular sectors. #DigitalGeometrySketchbook

@Rainmaker1973 https://t.co/mmX2HBHdue