# ワケあってこのカタチなの tv番組 フィボナッチ数 収斂進化 現代和算

他の正多角形ではどうなるでしょうか。

255 1323
2022-06-18

唐突に思い付いたモンタ×ミノなど米がワイやで、音声もトギレ跡切れ環境だったので難聴大喜利しかできずスマソ、線対称軸上でない対角線5本共点がある最小?正42角形の次という質問に備えて正84角形であったと思って2倍自明、8本驚天がない論文30以上6倍N正多角形しか書いてないから32とか聖典,教典,経(

0 0
2022-01-22

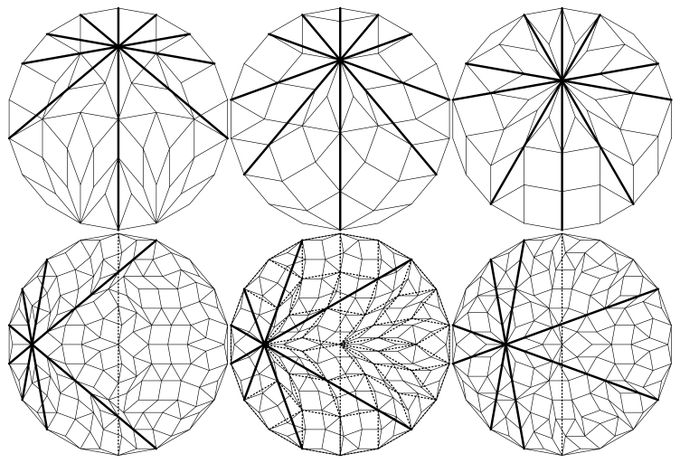
おっはー（死語）正多角形の対角線ふしぎ！遅れて関係ないかもですがhttps://t.co/mq74opT1NV 様紹介の論文から、正18角形の対角線5本共点（図上）と対角線4本共点（図下）が18回回転対称で添付図の3通りずつっぽかったので、一応菱型（と正三角形）タイリングで内分比も比較的わかりやすく(ないけど！

0 2
2022-01-20

これは、実像が１/１２の６ポイント万華鏡の画面や立体魔方陣のＤＮＡ配置と同じに見えますね。
リーマンの ∞ポイント 万華鏡 新発明！ 正多角形作図のメカニズム - 発想力教育研究所 素数誕生のメカニズム https://t.co/eCNqwdk8Xs

0 0
2021-11-20

ね(＾∀＾)プケラw
『必要は発明の母』と言う様に、箸1つ取ってもその形状に理由はあるのよねえw
自然界でも やら 等の様に、自然の作用、或いは環境への適応で必然的にそう成る(#収斂進化)と言う事がある件w

1 0
2021-10-22

正多角形デジタル陰陽魚は添付画像左のように端数セビレだと右の正2×奇数角形の半値ズレから暫定しました。あと黃＝灰＝桃＝水色部の面積は、それぞれ前述かの松角解析サブグリッド一番細長い菱形由来の二等辺三角形とかで説明可能として、星形含む一辺2の正多角形タイリングの中全てのピース分類を(終

0 0
2021-01-19

ルーローの正多角形からタチアワセもとい等面積変換で額縁に！弓形の所はサモアリナみンだけど正二倍多角形の等面積のところがまだホントか眠くて計算よくわからん

0 0
2020-04-02

（半径hの時針とより短く半径mにした分針の時計ベクトル終点間を結ぶ線分）水色のε:(1-ε)の内分点でトロコイドしたときに見かけの星型正多角形の頂点が丁度サイクロイドになるときの内分比(1-ε)/ε=12*m/hで、それがエピ外順でもハイポ内逆でも同じ（承前内外が間違ってた笑）気がする-ハイ全力スルー🧐

0 2
2020-03-18

面積比 π : n tan[π/(2n)] ってドコカで見た気がするけど、まあ円内接正多角形の添付図の部分でn→∞の極限で丁度円の面積の半分になるという何だっけか略。まあ俺のことだから菱形タイリング系の何かだろうけど、といいつつ未来の検索対策で思いつくまま用語を文字数制限分だけ並べて細工は流々あと終

0 0
2019-10-14

正多角形グリッドの整角ベースでない整辺系は円弧の三等分とかが目無しになるので、円弧は最大四等分される中から数合わせで選ばなければならない七宝グリッド！あとはヒポクラテスとかアルベロス的な三日月オペオペの実だっけかが出来るかだけ心残り.https://t.co/m8NX1bB8k4 https://t.co/I4KVEvnhlU

0 0
2019-08-29

あと円弧的には六芒星を2つ入れるとピッタリかも（よく計算してない）ルーローのエンコだけに謎。3等分の際には添付図の紅葉饅頭2つの領域だと飛び地になるので、ハジキやミハジやクモワだっけかのようなT分割がいいかも。つまるところ正多角形グリッドに沿った面積等分割と弓形の相似形の数合わせ面白

1 11
2019-08-28

『奇書の世界史』https://t.co/QeO6xJ5ft8 様が竜巻巴にお気付きになられてたようでしたGJ、もっと正多角形グリッドに沿った等分と円弧弓の相似数合わせが見たいけど五等分様のもホボ大喜利状態で,でも立体は面白いですね算数星人豆腐様「5回の切断で直方体を8等分しましょう」https://t.co/fNsGSQp0Ln

0 0
2019-08-26

定義曖昧だったCresCres7を凹平行六辺形に圧縮したら添付図1の謎クリーチャー1単位ジグザク境界で出来ました、さらに添付図2のCresCres11でコノ系はただの正22角形ベースのパクリンピックhttps://t.co/vVTZwJFcXA みたいなものだと結論。等距離グリッドで到達できる正多角形同士の額縁タイリング応用略

1 2
2019-03-10

せっかく4年越しに同じような問題で頑張ってる外人様に特に伝えることも無ければ何を含んでいても仕方ないか、カギンチョはTwilog＆Google検索にかからなくなるのが辛いので様子見ながら又出戻り秦モト春樹略。歯車型とか正多角形ポリゴリング双対パターンブロック欲しすぎる、最適サイズや数は不明(終

1 2
2019-01-27

ａｐｕさんはじめまして！すごい人っぽいオーラでてて、僕は恐縮です、引用リツイートありがとうございます！
菱形（＆正多角形）タイリングは、僕は2020TOKYOオリンピックのエンブレムの野老さんから知って、荒木さん@.alytileの情報などをふまえて僕は色々パクってます。
正九角形は従来手法ですが8!

0 3
2019-01-10

（一般化ギリータイルでの放射状平面充填こそ添付図左のパックマン格子グリッドや、右の正多角形くねくねタイリングの為だけに菱形じゃ全然なく使える新しいタイルの全数列挙が必要だと現状は思いましたが、面積がどうとか言う話にはちょっとなりにくく応用性が見えないため保留ということで

0 0
2019-01-04

ギブアップですT先生！というDMはさて置いて、9も添付図の正11角形でも綺麗な周期性は見えないし、正多角形の一部を削るパックマンでもこのアニュラス内ではどうしていいか分からず。とりあえず正奇数角形二個卵はその2倍の正偶数角形から平行な2辺を消してクッツけただけで、次の正偶数角形で頼んます

0 0
2019-01-03

あけましておめでとうございます（Twitter重くなる前にフライングゲット！
偶数正多角形の方が添付図（正16角形例）のように直感的にできました！
特に2×奇数辺の正多角形だと、お教え頂いたPDF https://t.co/Lmhc5ZQ3Hz 的な対角線の関係から、タイル数を減らせそうで失敗！→https://t.co/mWzzgYU1Pm

1 1
2018-12-31

くない衒学ゲーム略、組合せゲーム理論的には素晴らしく有用だと思うので、是非ニムイマケカチや簡易版や複合局面の保留手も含めて検討が流行って欲しい（やらない）。添付図の正多角形の高さが同じ長方形への変換には公式的な物がありそう、無ければほぼ自明な3・4・5・6・10・12（の倍数？）以外無理

0 0
2018-12-29

三角格子とかで拡張したら六芒星じゃなくなるわ、添付図もシルエットパズルは角度で合わせて 長さ重視みたいな事を示している気がしたXmath。ダートをうまく使うためには、凧形タイリングと正多角形の合わせ技とか極めないと無理ゲー感、できそうな人といえばさっきゅんさん(謎https://t.co/p1nhgTsqqG

0 0
2018-12-25