# エピオルニス モナーク作戦ss artwork 絵描き友達がほしい 絵友希望 創作同盟 イラスト王国 illustrations drawing 絵描きの輪 digitalart artistontwitter 秋の創作クラスタフォロー祭り 勉強垢 integrral 積分 数3 受験勉強 サモンズボード スライム娘版深夜の真剣お絵描き60分一本勝負 絵描き人 art イラスト 創作 comic 数学 integral 媒介変数 絵柄が好みって人にフォローされたい 絵描きさんと繋がりたい 平面 数2 絵師

【卵比較】地上最大の鳥と考えられる絶滅種 の卵化石（中央）。ウィーン自然史博物館で撮影。30センチ大で鶏卵の約180倍の体積があります。手前右下が鶏卵。左隣がダチョウの卵です。エピオルニスは恐竜と鳥をつなぐ存在だったのかもしれないですね❗️

7 20
2020-12-11

友人からのお題がドーナツだった
いまのくさは1.5倍ぐらい体積がある

1 22
2020-12-06

(腕は再び白帯へとほどけいく。しかし今度はその「量」がとてつもない)

(腕どころかユミエの身体の体積より明らかに膨大)

(むしろそれが、折り畳まれていた「義手・白帯姫」本来の姿であった)

あ！あぁ…

(思わずヒカリがたじろぐ)

(起き上がった「ソレ」がヒカリを見たからだ)

2 13
2020-12-01

ごはんたべたあとにFTD
新規設計の軽巡
139298コストに9218㎥

で、小さく濃くがモットーの私めとしては
ほんとにうまくできたんか？と
アプデ対応を行った前級と重巡とで比較

したら1FirePower出すのにかかったコスト、体積共に新規軽巡より前級のがよい…

まだ無駄があるってことだな…

0 2
2020-11-30

【終末紹介】No.11
"ティアマト”四条海未

それは尋常の攻撃を無為と化す、理論流体の肉体を持つ。
それは極微の間にすら浸透し、押し流し、大地を大海に変える体積を持つ。
それは自身の由来を知らぬまま、無限の戦闘分岐を有する武術を修める。

星を蒼に帰す滅びの波。それが”大海”による終焉である

1 3
2020-11-28

[新作・共著] 相模湾深海に棲むChilostomella属底生有孔虫の体内から多数のキチン質構造を発見し、その分布を3D再構築で明らかに。その機能はまだ未知だが、細胞質の表面積対体積比を増やすことや触媒作用などの可能性を議論。 J Euk Microbiol 誌に掲載: https://t.co/7hd8Q2rLrc

2 9
2020-10-31

なお、１FでTP70稼いでシエルのTPスキル使えばとりあえず２Fは突破できるんじゃないかと思い、TPソウル4体積みパーティーで挑んだ結果がこちらです。

0 0
2020-10-24

妹子が誕生日らしいです。
らす民はしらすさんのいる方角に向かって礼拝してねるねるを奉納してあげてください。
親知らずの分体積が減った妹を今後ともよろしくお願いします。

最後は睡眠導入してくれるしらすさんでのお別れです。
では、良い夢を。

4 13
2020-09-30

データ入稿完了！昨日の混乱は何？って感じであっさりできました。出力用に1つオブジェクトを置きその設定を人形の高さに設定し一緒に書き出します。パーツは組み合わせて体積が少なくなるように組み合わせます。ポリゴンを減らしてなるべく軽いデータにします。
この子は高さ30ｃｍ、アイ16ｍｍです。

1 12
2020-09-28

お題「男装・ボーイッシュ」


説明しよう！このスライム娘はスライムなので容姿を自由に変形できるが体積を変えることはできないため男装するにあたっておっぱいなどの分をどっかに分離しておかないといけないのである！

24 62
2020-09-27

脳は人間の約4倍の体積があるから
高度な知能を持ってると思われる

脂肪組織、頚椎のクッション、
下肢の逆間接により
落下してもダメージはほぼない？

脂肪組織に対して骨格が小さいから
すごく重いし動けなさそう
つまり、この空洞には
筋肉組織が詰まってる？
なぞだなぁ

0 2
2020-09-24

　　　　　　　　　 　
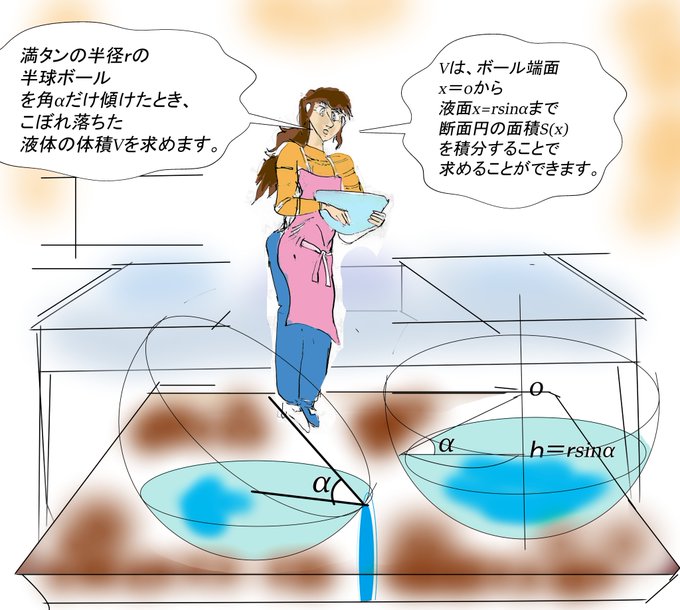
半径ｒの半球を角αだけ傾けてこぼれ落ちた水の体積。これは（rの二乗－ｘの二乗）をｘ＝rsinαまで積分することで得られます。

30 64
2020-09-20

まだ入れることを主張してくるねこしんしんさん 体積だけだと容量オーバーだけどバランス感覚がとても良い

13 38
2020-09-15

ハードサーフェスものでよく見るこの謎凹みの意図はなんなのだろうか。
体積を減らす軽量化目的だろうか？

1 8
2020-09-10

おっと、片付けのワナにまんまとハマったようですニャ(笑)

昔の本・ノート・プリントなどなど、体積の割に情報量が多い媒体は沼ですニャ～💦

0 7
2020-09-02

自推で！
デフォ衣装も冬服も体積凄いのでライトあたりを守りたいです⚾️
羽があっても5センチくらいしか浮遊出来ないのでゲームは壊さない！

0 3
2020-08-19

　　
X/a+Y/b+Z/c＝１の1/a、1/b、1/cの
二乗和平方根の逆数を計算すれば、平面に
降りる垂線の長さを算出できます。
またa,b,cは３軸の切片なので、これらを使えば
３角錘の体積を計算できます。
平面に下した垂線の長さで、錐体体積を割れば、
斜面の面積がわかります。

10 29
2020-08-15