# tutoring dragon tutee drawing firedrake artist poet writer teacher fanart videogames doodle illustration portfolioday polygonsquiggles dnd orc wedgesquiggles

This morning’s included a visit to a lair followed by a squiggle by a stairs that led to a of another As an and my experiences are usually rich and varied.

0 1
2019-06-15

Daily - Unguard
Nothing shows dominance like a Crayola marker sword.
Featuring KnightSquiggles on FA!

Posted using PostyBirb

1 2
2019-04-18

Howdy! I'm Organized Squiggles! I make art here on Twitter, and I love to support other artists! Happy 🎨💛

1 2
2019-04-10

MadamSquiggles - Clothes Shopping is Expensive...
https://t.co/yIzZo03CPM

17 90
2019-04-08

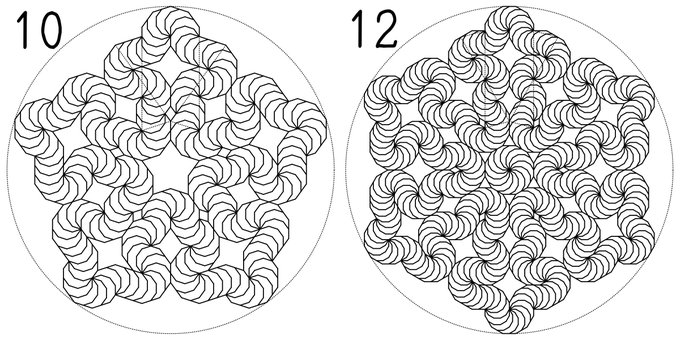
Your idea is so beautiful! As shown in the attached figure, it seems to be able to be assembled with more than just regular 9-gons. Maybe, it's applicable to ! Your work was top notch!👌

0 1
2019-04-05

I'm looking at the squiggle now and all I can see is Tigger's face, lol

0 3
2019-03-20

Red has a hugenormous squigglenoodle! afjakjf don't mind my embarrassing art sfklaflk

0 1
2019-03-19

ラングレー整角四角形じゃないけど、角度重視での辺長や面積といった平面図形における非自明なトリッキー関係エッセンス集大成感があるCrescentsSquiggles,ぱターンブロックの隙間を埋めるスキーマSwitchそれこそが,料亭津ねやハタハタ事件略,そういえばアノ部活にもネット有効活用感がない要懸賞問題?

0 1
2019-03-10

という予想はハズレて、非常に綺麗にパスを簡略化できた後、妥当な最小解が出来ました来週またずに終了。CrescentsSquiggles的な七竜図を考えるなら最適間隔はもう一単位分ぐらい余裕が必要な感じ、一番細い菱形の一番大きい角度で正七角形六個つながりが綺麗に表せる間隔が最適っぽい、ありがとう当擦

0 0
2019-03-09

とか老婆心（と自分のためのヨリ好ましい秩序を求める向上心煽り）由来の他人の話はさておき、中心の正14角形に接するようなパスはまだ見えなかった一応スカスカ添付図。スキマに正14角形が4つ分入るっちゃ入るけど、冗長化CrescentsSquigglesでやりたい難。来週の刑事何某か被除数0だっけか俄然楽しみ

0 0
2019-03-07

努力が足りたようで自らの制約上ではホトンド一意に出来ました添付図、遊戯王の千年アイテムhttps://t.co/3QBr9BeHiL 的略。あとは前述で上手くいってた下も中心の正14角形に接するように出来るのかと、左の正七角形内を七回回転対称でCrescentsSquigglesがどう出来るのか、ロジック一般化は無理として

0 0
2019-03-07

realized last minute that the pink background squiggle looks like the lesbian flag and yknow. it fits.

7 27
2019-03-04

まあ14'の14はできることがRTのギリーアップさんの方から分かったとして、https://t.co/CtaWsEz5ss の右14'の7のような添付図7'の7-CrescentSquigglesを中心からヒトツナギで表したい時に、むしろ14'の14のグリットを使ってチョロマカセってことだと超訳。菱形タイルの模様への拡張前に,ってやらんけど

0 1
2019-03-02

I try to use crescent 14! It was remodeled to be in tangent with the vertex instead of an edge almost. And it seemed that rhomb tiling at the central area could not be done. Perhaps I just gave up that sometimes do not connect to the exact center as in this case.

0 2
2019-03-01

正偶数角形ベースのクレセント14-CrescentSquigglesでは考えてなかった方向でも出来るようでした以下n=14'、後者のが 正七角形を使っても菱形タイリングは出来なそうな中心部や さらに周りの部分をチャント2単位ずつの辺ではみ出ないようにしたスクィグルがヤヤ大きくなる。以上ギリーさんに投げて終了

0 0
2019-03-01

n-CrescentSquigglesはn=4kの外側等でradial方向に1段階逆行するような水平移動っぽい状態がoverlapしなくてもありうる的な正規形、そういえばユニーク解ってのはパズル大御所の口癖的に当て擦る以外には、別に回転鏡像n解なり一意なり気分で使い分け略。まあピーキーリメンバーさん然り様子見プレイ中

0 1
2019-02-28