ほりたみゅ(bskyかmastodonに居ます)さんのイラストまとめ

今度はさっきと順番を逆にして回転行列Rで変換してから行列Aで変換してみます. 楕円の形は変わりませんが, 楕円の色相が変化しています. この例でも固有ベクトルが現れたり消えたりします.

固有ベクトルの現れる所を見てみます. 固有ベクトルが重なれば行列RAは対角化不能になります. 対角化不能の例としては{{1,1},{0,1}}(ずり変形)があります. 固有ベクトルが直交すれば行列RAは対称行列です.

先ほどの行列Aで変換してから回転行列Rで変換してみます. 行列RAの固有ベクトルは回転角度によって消えたり現れたりします.

2次元の回転行列Rに対してこの方法で固有ベクトルを探してみますが, 当然ながら恒等変換以外では見つかりません. (単に回転させるだけだと変換前後で重なって分からないので適当な定数kを掛けて拡大してます.)

LaTeXでこのフォント出したい時ってどうすれば良いんだろう

このインボリュート曲線を歯面にすればインボリュート歯車の完成です. 基礎円と歯底円が一致してますがこれは本質でないので問題ないです.

その動画がこれです. ケーリー変換(z-i)/(z+i)によって上半平面が単位円盤に移ってます.

残り最後のNS軸回転は少し考えたら簡単で, メビウス変換を表す行列はこのようになります.

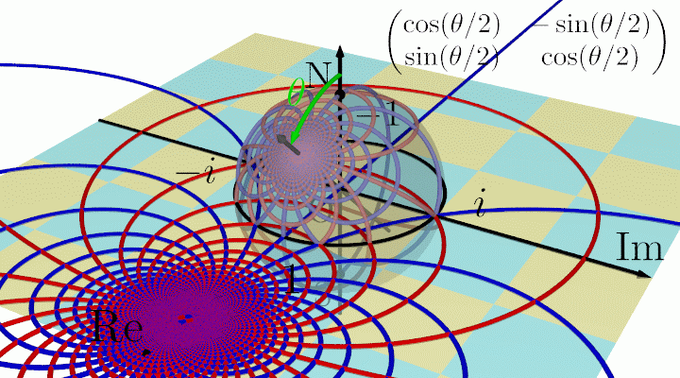
Im軸周りのθ回転を表すメビウス変換の行列Q(θ)はこのようになります. 良く知ってる2次元の回転行列と同じになります.

円を円に移す変換といえばメビウス変換です. 実はRe軸周りの任意の角θで回す変換を表す行列P(θ)は右上の行列になります. (計算ガリガリすれば確かめれる)