創作同盟のTwitterイラスト検索結果。 570 件中 15ページ目
#創作同盟 #drawing
#絵描きの輪 #artwork #絵描き人 #art #イラスト
#絵描きさんと繋がりたい #創作 #illustrations
#art #イラスト
#digitalart #ArtistOnTwitter
#秋の創作クラスタフォロー祭り
円柱を斜めに切った体積を求める問題xをパラメーターとした面積比から、積分式を立てます。
#創作同盟 #絵描きの輪 #artwork #絵描き人 #art #イラスト #絵描きさんと繋がりたい #illustrations #art #ArtistOnTwitter #秋の創作クラスタフォロー祭り
半径rの半球を角αだけ傾けてこぼれ落ちた水の体積。これは(rの二乗-xの二乗)をx=rsinαまで積分することで得られます。
#接線 #tangent #tangential #創作同盟 #drawing
#art #イラスト #数学
#digitalart #ArtistOnTwitter
#秋の創作クラスタフォロー祭り
#絵柄が好みって人にフォローされたい
y=ax+bのa,bを規定する座標系をパラメーター空間といい、ハフ変換等の直線補間技術において、重要な意味をもちます。
#数3 #創作
#創作同盟
#digitalart #ArtistOnTwitter
#絵描きの輪 #artwork #絵描き人
#絵描きさんと繋がりたい #illustrations
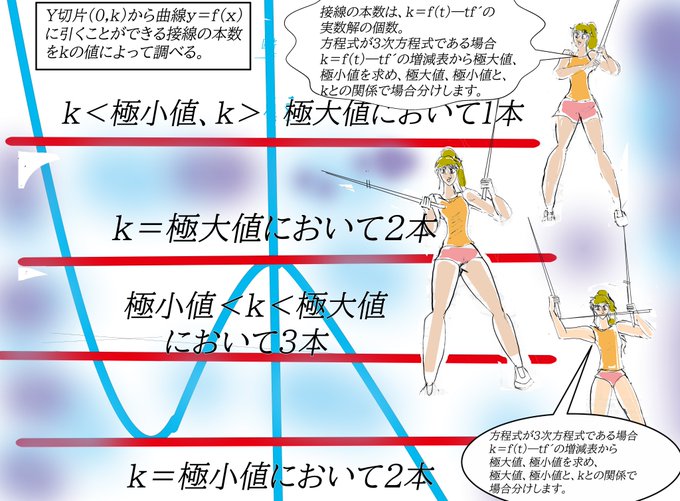
(0,k)を通る接線の本数を求める問題。接点tからY切片に導く関数f(t)を想定して、f(t)の極大値、極小値と、y=kとの関係から、接線の本数を求めます。
#poweredsuit #パワードスーツ #アシストスーツ
#drawthisinyourstyle #ArtistOnTwitter
#插畫 #插画 #繪畫 #скетч #рисунок
#絵描き人 #絵描きの輪 #創作同盟 #絵師
#illustrations #drawing #artwork
赤い色のパワードスーツ。通常の3倍の速度で荷受け作業、積下し作業を行います。
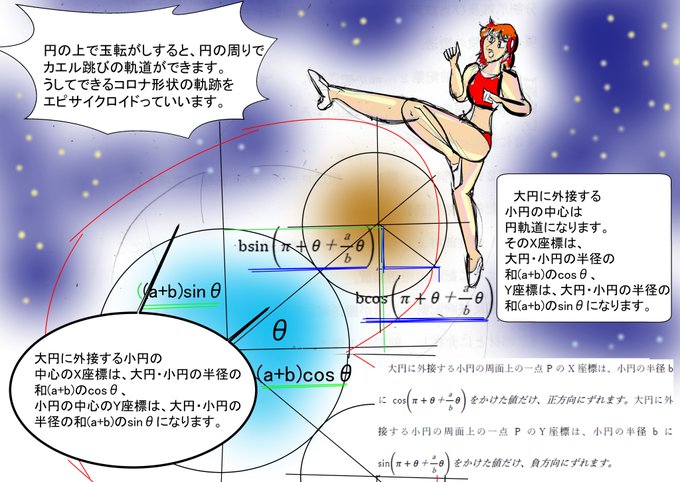
#epicycroid #エピサイクロイド #絵描き人
#絵描きの輪 #創作同盟 #ocart #oc #illustrations #drawing #artwork #絵師 #illustration #数学
エピサイクロイドの場合、小円の周の座標は、bsin(θ+π+b/aθ)、bsin(θ+π+b/aθ)になります。πは初期位相、a/bθは、θに径の比率を乗じたものです。
#区分求積法 #Piecewisequadrature #創作同盟 #artwork #絵描き人 #くノ一 #絵描きさんと繋がりたい #オリキャラ #忍者 #ninja
(k/n、1/n)の旧バージョン。積分のΔxというのは定義域[a,b]をnで割ったものです。a=0、b=1にしたのが
Δx=1/n、xがk番目に位置するとするとx=k/nです。
#区分求積法 #Piecewisequadrature #創作同盟 #drawing #絵描きの輪 #artwork #絵描き人 #art
#絵 #絵描きさんと繋がりたい #オリジナルイラスト #創作 #オリキャラ #忍者 #ninja
#イラスト好きな人と繋がりたい
区分求積法の問題の具体例です。1/nを積分式のdxと考えて計算します。