なんちゃってダイハツウィンカーのようなイシパカの最後ｯﾍﾟ断末魔＠番組表ＥＰＧ用アライブ外字フォントさんのイラストまとめ

@shinshu_us @no_TL まあ色々いいてえことはあるにしても、正七角形ベースのピースで√7作れるならヤルしかナイト。なお中心線上ハジッコに完全に一番トガッてる二等辺三角形での面積同じ端数の形が鋭角VS鈍角みたいな、例によって細かい所は全く数えてないしツジツマ合わせ最適化もしないけど、以上 #現代和算 「七之七」

@shinshu_us @no_TL ひたすら鯛焼きトイウカなんでしょホットケー略を斬リ続けるマンと化している今日この頃、（添付画像は五之五だけど）とうとう七之七の目処が付きました19時頃後述。ほんとコレ「クロネッカー・ウェーバーの定理と証明のあらすじ（その１）」https://t.co/K7EBdRIhL9 のおかげッテカ見たことありそうな

@shinshu_us 正多角形デジタル陰陽魚は添付画像左のように端数セビレだと右の正2×奇数角形の半値ズレから暫定しました。あと黃＝灰＝桃＝水色部の面積は、それぞれ前述かの松角解析サブグリッド一番細長い菱形由来の二等辺三角形とかで説明可能として、星形含む一辺2の正多角形タイリングの中全てのピース分類を(終

@shinshu_us 何も考えずHintzTorus真ん中でやってたけど、個人的オススメ鯛焼きカットは添付画像右にしておきます謎の強い主張。尻尾と背びれとクチとピラニアみたいな、そういえばタイなんて刺身にオロされた状態しか見たこと無いし似たようなもんか違うか。さて真ん中が菱形ナンコ分かというのが後述の本質情報で

端数ちがってたサイレント修正！いやー最近も計算がオボツカなくてツイ消し細胞アリマァス！あとは任せた！！

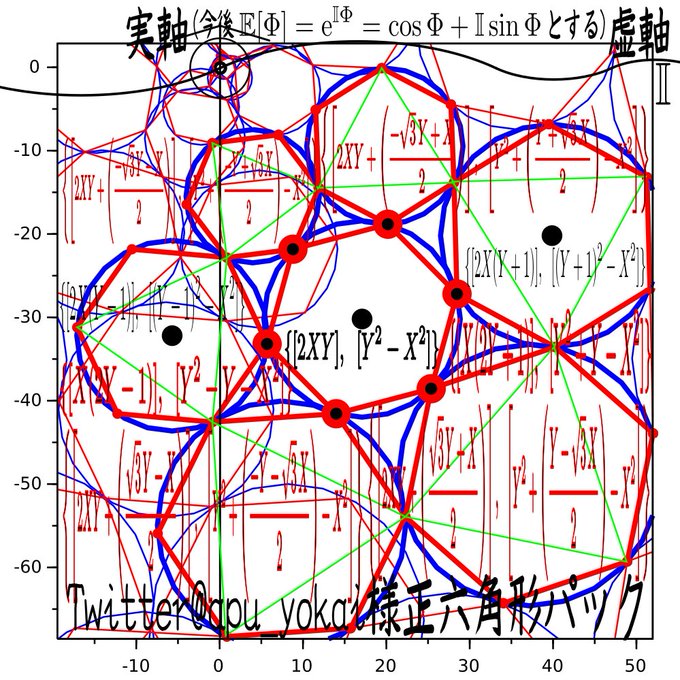
@shinshu_us @no_TL 正六角形の各頂点毎の周りであるベクトルが外120度回って戻ってくる知らんけど正六角形七接定理があるとはいえ、互いに円が接する場合は中心間線分上に接点があるという設定とはいえ

@shinshu_us @no_TL 縦置き正方格子のが綺麗な座標になるし定数倍の不定性の比例係数倍Wとかやってないけど、z^2まわりのr=|z|共形変換おそろしやhttps://t.co/Drv2HvBIEc に関係した恒等式https://t.co/ILXKpK0LvQ も発見、横置き長方形格子に一般化した座標公式が良さそう.互いに接する円への拡張は半径イジリあと逆変換

@shinshu_us @no_TL 荒木アプ様の離散○反則関数だっけか複素距離冪例変換とかで良くね比例係数WZ*Z^2=W*(x^2+y^2), WZ*Z=W*√[x^2+y^2], 算変象図WZ/Z^2=W/(x^2+y^2)*(r\\[x\\y])的な確かにその点までの距離で割ったら円周上に恒等写像か、的なやはり基準単位円の内側だけで大体無限周期一周分を表せ感じじぇ虚軸を波平線

@shinshu_us @no_TL Σじゃねーな漸化式、名前大喜利中かのナントカ様の方の数値例でHerry erisyq_17/status/1292816240847646720様のp_kが満たす複素式を定式化ホントカ、Z_0に掛けられる回転は動径固定の偏角変化のみで係数0非依存状態にした上で、残りの円周上ベクトル回転の総和も何周かで0みたいな恒等式的な知らんけZ

@shinshu_us @no_TL https://t.co/yKre919X0G 的な股ABCで内心円半径が√[ABC/(A+B+C)]ということと、円7つの子分でも相似になるように（接するかとか不明だけど）すると添付図の双対になる気（複比じょのいこ双似とでも仮称するか）さらに略