デッドライナー：理系創作にいそしむ弁理士さんのプロフィール画像

デッドライナー：理系創作にいそしむ弁理士さんのイラストまとめ


創作活動に勤しむ弁理士です。ギャグ、SF、メカアクション。理系に関する様々な創作世界にあなたを誘います。
novelup.plus/story/760789084
novelup.plus/story/99979863
pixiv.net/artworks/119

フォロー数：3641 フォロワー数：3858
# 接線 tangent tangential 創作同盟 drawing art イラスト 数学 digitalart artistontwitter 秋の創作クラスタフォロー祭り 絵柄が好みって人にフォローされたい 数3 創作 絵描きの輪 artwork 絵描き人 絵描きさんと繋がりたい illustrations イナズマン ライジンゴー 昭和特撮 区分求積法 忍者 ninja くノ一 poweredsuit パワードスーツ アシストスーツ drawthisinyourstyle 插畫 插画 繪畫 скетч рисунок 絵師 epicycroid エピサイクロイド ocart oc illustration cycroid サイクロイド 定積分 極限 数列 seguence オリキャラ 物理 ローレンツ力 lorentz 逆起電力

　
　
　
　　
　　　
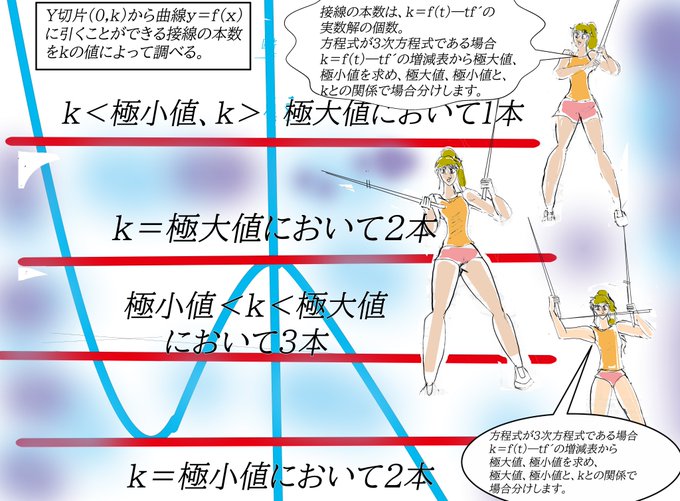
(0,k)を通る接線の本数を求める問題。接点ｔからＹ切片に導く関数f(t）を想定して、f(t）の極大値、極小値と、ｙ＝ｋとの関係から、接線の本数を求めます。

12 31
2020-09-16

　　　
　　　
　　　
悪人に女の人が追われていて、こんな車に乗って主役が「どうしました！」って登場する。「追われているです」って訴えて誰も車につっこみをいれない。それが昭和特撮です。

2 32
2020-09-13

　　 　
　　　　
　
謎の関数f(x)の(t,f(t))で接線が接している場合、
Ｙ軸と接点とがなす三角形の面積と、
Ｘ軸と接点とがなす三角形の面積との関係から、
謎の関数f(x)を求めることができます。

1 13
2020-09-13

　　
　　　　　　　　　　
４ｎ！を３ｎ！で割ることで（３ｎ＋１）から（３ｎ＋ｎ）までの２項式の数列になります。ｎのｎ乗でくくると１／ｎ乗が１／ｎを相殺します。すると積分式に変換できます。

18 26
2020-09-12


　　　　　 　　
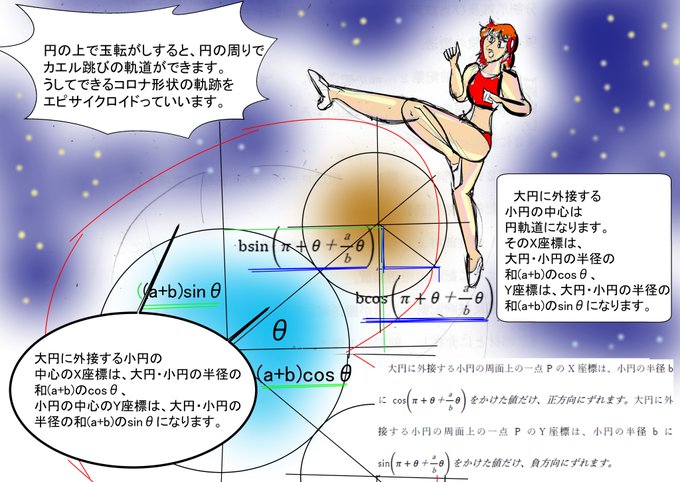
エピサイクロイドの場合、小円の周の座標は、bsin(θ+π+b/aθ)、bsin(θ+π+b/aθ)になります。πは初期位相、a/bθは、θに径の比率を乗じたものです。

15 40
2020-09-10

　　 　　　
回転する円の中心は地面の水平移動します。その座標は(aθ、a)でありＸ座標はθに応じた値になります。円周上の一点はＸ座標、Ｙ座標からasinθ、acosθをひいた値になり、カエル飛びの軌道をなします。

34 54
2020-09-09

　　　　　
　　　
　　
logn!と、部分積分の積分値との不等式を証明する首都大東京の過去問。logn!が何番目の項までの総和なのか、またこの総和が、どの範囲まで面積を上回るかが問題になります。

1 15
2020-09-06

　　　　　 　
　
鉛直方向に向かう磁束密度Ｂの磁界中に、角度θをなす斜辺があり、ここに敷かれたレールで転げ落ちるシャフトをキャラクターにしました。転がるときの逆起電力により速度を０にします。

14 32
2020-09-06